Statistic & Probability

Computing and Data Science
A statistic is a quantity calculated from a sample.

The probability of an event \(E\) is: \[P(E) \in \left[0,1\right] \]
  • Probability of \(0\) means no chance of happening
  • Probability of \(1\) means guarenteed to happen

Monte Carlo Coin Flip    

Flips: 0

Monte Carlo Coin Flip, Normalized    

Flips: 0

Statistics


Probability

Theoretical:
P(H) = 0.5
P(T) = 0.5
The probability of event E occuring is \[P(E) = \frac{\text{Number of ways E can occur}}{\text{Total possible outcomes}}\]

🎲 Monte Carlo Die Roll    

Rolls: 0

🎲 Monte Carlo Die Roll, Normalized    

Rolls: 0

The Cat Machine has a random probability of generating a cat.
Try the machine and then guess \(P(\text{cat})\)!
→

P(cat) =
Create a 6x6 grid with both the rows and columns labeled 1 through 6.

  1. In each cell, write the sum of the row and column. For example, row2-col5 should have a 7 in it.
  2. How many unique sums are possible?
  3. How many times does each sum appear in the grid? Make a normalized histogram.
  4. Experimentally collect as much data as you can by rolling two dice and recording their sum. Create a histogram of your data and compare it to the theoretical distribution.
  5. Determine a function to fit the distribution from your experimental data.

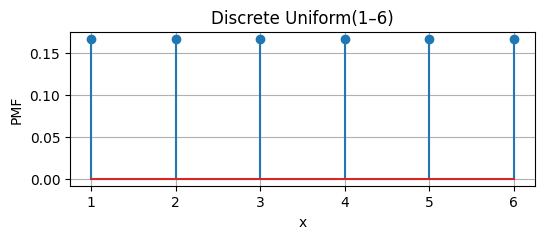
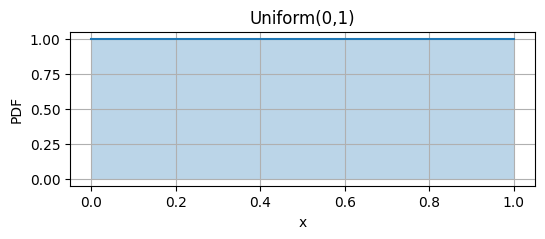
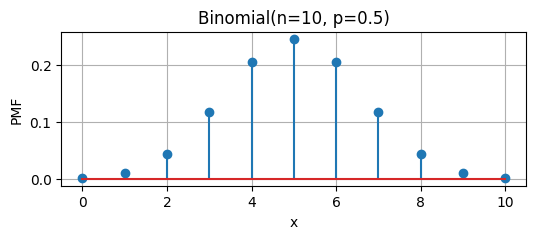
Discrete v. Continuous

Discrete Continuous
Flipping a coin Time a trip takes
Rolling a die Length of a broken stick
Drawing a card Temperature on Dec 19
Choosing a person Height of a person
DiscreteContinuous


Probability of rolling an even number = \(\frac{1}{6}+\frac{1}{6}+\frac{1}{6}\)



Probability of value between 0 and 2 = \[ \int_{0}^{2} f(x) \ dx \]

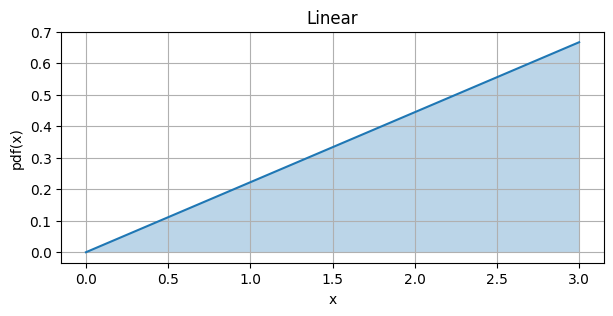
Probability of value between 1 and 2 =





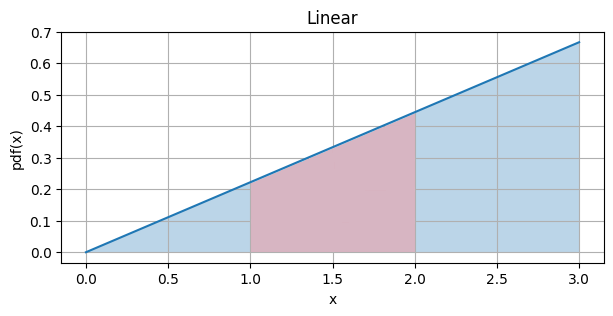
Probability of value between 1 and 2 = \[ \int_{1}^{2} f(x) \ dx = \]

Broken Stick Problem

Given a stick broken at two random places, what is the probability that the three pieces can form a triangle?

©2025 Jedediyah Williams
This work is licensed under the Creative Commons
Attribution-NonCommercial-ShareAlike 4.0 International License.

To view a copy of this license, visit https://creativecommons.org/licenses/by-nc-sa/4.0/.