CDS

Graph Theory

Computing and Data Science

A graph is something with this structure:

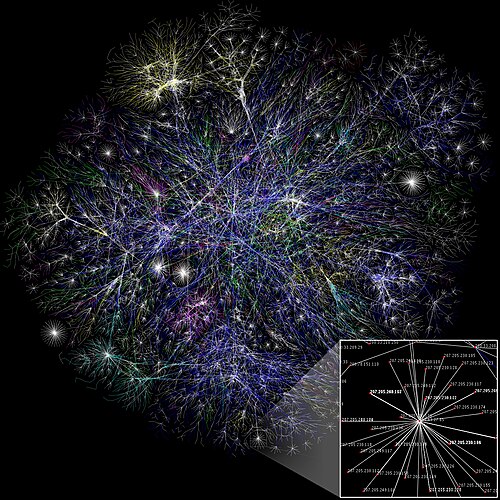
A graph is a pair of two sets such that the second set is a set of two-element subsets of the first set.

\[ G = (V, E) \]

\(G = ( \)
	\(\{a,b,c,d\}\)
\(,\)
	\(\{ \{ a,b \}, \{ a,c \}, \{ b,c \}, \{ c,d \} \} \)
\( ) \)

Vertices

Edges

\(G = ( \)

\(\{a,b,c,d\}\)

\(,\)

\(\{ \{ a,b \}, \{ a,c \}, \{ b,c \}, \{ c,d \} \} \)

\( ) \)

A graph is composed of vertices and edges.
\(G = (V, E)\)

A vertex does not require an edge.

There can be multiple edges between vertices.

No loose edges allowed.

The picture is just a picture.

\[ G = ( \{a,b,c,d\}, \{ \dots \} ) \]

\[ G = ( \{a,b,c,d\}, \{ \{b,c\},\{b,c\},\{c,d\} \} ) \]

Adjacency List

\(a\)
\(b\)	\(c\), \(c\)
\(c\)	\(b\), \(b\), \(d\)
\(d\)	\(c\)

Adjacency Matrix

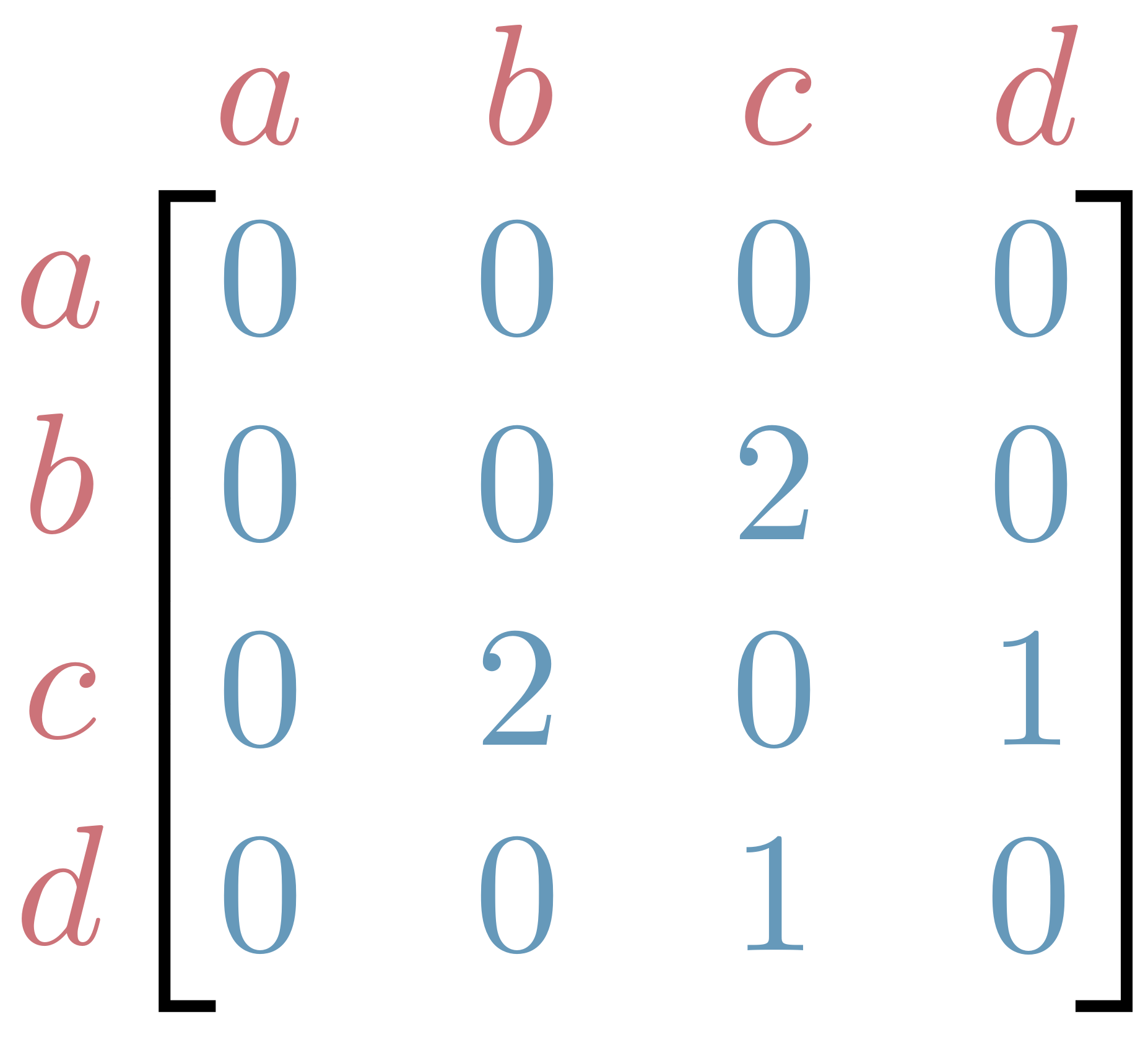
Adjacency Matrix


\[ \begin{bmatrix} 0 & 1 & 0 & 0 \\ 1 & 0 & 1 & 1 \\ 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ \end{bmatrix} \]	\[ \begin{bmatrix} 0 & 0 & 0 & 2 \\ 0 & 0 & 2 & 0 \\ 0 & 2 & 0 & 1 \\ 2 & 0 & 1 & 0 \\ \end{bmatrix} \]	\[ \begin{bmatrix} 0 & 1 & 1 & 1 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0 \\ \end{bmatrix} \]

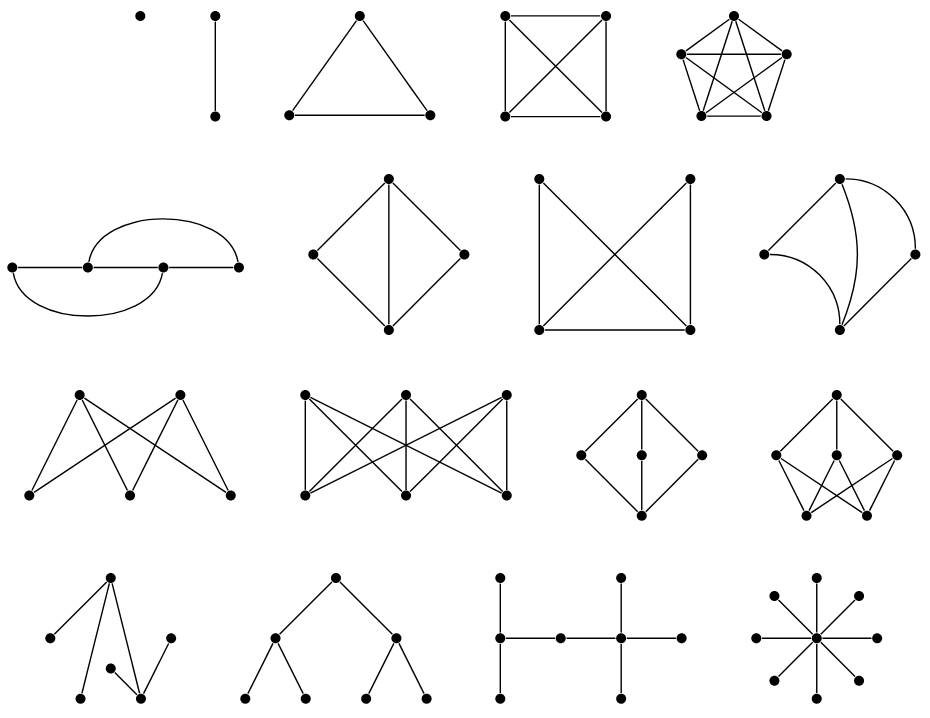
Practice

Write the adjacency list and adjacency
matrix for the graph below.

Practice

Draw a graph corresponding to the adjacency matrix: \[ \begin{bmatrix} 0 & 1 & 1 \\ 1 & 0 & 0 \\ 1 & 0 & 0 \end{bmatrix} \]

Complement

Given graph \(G=\{V,E\}\), the complement \(\overline{G}\) is the graph with:

The same vertex set \(V\)
Edges between vertices \(\{u,v\}\), iff \(\{u,v\} \notin E\)

Complete Graph

A complete graph is a graph where every
vertex is connected to every other vertex.


\(K_{3}\)	\(K_{5}\)	\(K_{12}\)

Bipartite Graph

A bipartite graph is one where vertices can be separated into two sets such that no edge connects vertices from the same set.


		\(K_{3,2}\)

Fundamental Graphs

Complete	Complete Bipartite	Cycle	Path

\(K_6\)	\(K_{4,3}\)	\(C_6\)	\(P_6\)

Fundamental Graphs

Star

\(S_6\)

Fundamental Graphs

Star	Star

\(S_6\)	\(S_6 = K_{1,5}\)

Walks, trails, paths, and cycles...

A trail is a walk that does not repeat edges.

A path is a walk that does not repeat vertices.

A cycle is a path that starts and ends at the same vertex.

A walk is a sequence of adjacent vertices.

A trail is a walk that does not repeat edges.

A path is a walk that does not repeat vertices.

A cycle is a path that starts and ends at the same vertex.

A walk is a sequence of adjacent vertices.

A trail is a walk that does not repeat edges.

A path is a walk that does not repeat vertices.

A cycle is a path that starts and ends at the same vertex.

A walk is a sequence of adjacent vertices.

A trail is a walk that does not repeat edges.

A path is a walk that does not repeat vertices.

A cycle is a path that starts and ends at the same vertex.

A walk is a sequence of adjacent vertices.

A trail is a walk that does not repeat edges.

A path is a walk that does not repeat vertices.

A cycle is a path that starts and ends at the same vertex.

Tree

A tree is a connected graph with no cycles.

An Eulerian trail is a trail that uses each edge exactly once.

A Hamiltonian path is one that visits every vertex exactly once.

Equal or Isomorphic

Graphs are equal if their vertex and edge sets are the same.

Graphs \(F\) and \(G\) are isomorphic if there is a way to map the vertices from \(F\) onto \(G\) and get a graph equal to F.


\(F=\{ \{a,b,c\}, \{\{a,b\},\{b,c\},\{c,a\}\} \}\)	\(G=\{ \{x,y,z\}, \{\{x,y\},\{y,z\},\{z,x\}\} \}\)

Subgraph

Given a graph \(G=(V,E)\),
the graph \(G'=(V',E')\)
is a subgraph of \(G\) if \[ V' \subseteq V \text{ and } E' \subseteq E \]

Practice

Given the graph \[T = \{\{w,x,y,z\}, \{\{w,x\},\{x,y\},\{x,z\}\}\} \] Draw \(T\) and all of the possible subgraphs.

Weighted Edges

Weights are values associated with each edge.

Minimum Spanning Tree

The minimum spanning tree of a graph is a tree that spans all vertices with the minimum weight possible.

Kruskal's Algorithm — Minimum Spanning Tree

Given a connected graph, find its minimum spanning tree.

Create list of edges and weights
Sort edges by weight
Initialize a graph with the vertices and no edges
For each edge in list of sorted edges:
1. If it would create a cycle, skip edge
2. Otherwise, add the edge to the graph
3. If all vertices are connected, you're done

Directed Graph

Graph	A pair of two sets such that the second set is a set of two-element subsets of the first.
Equal	Graphs \(G=(V_{G}, E_{G}) \) and \(F=(V_{F}, E_{F})\) are equal if \(V_{G}=V_{F}\) and \(E_{G}=E_{F}\)
Subgraph	Graph \(G'=(V',E')\) is a subgraph of \(G=(V,E)\) if \(V' \subseteq V\) and \(E' \subseteq E\)
Isomorphic	There is a mapping \(f:V_1 \to V_2\) such that \(\{a,b\}\) is an edge in \(G_1\) iff \(\{f(a),f(b)\}\) is an edge in \(G_2.\)
Walk	A sequence of vertices where \(v_{i}\) and \(v_{i+1}\) are adjacent.
Trail	A walk that does not repeat edges.
Path	A walk that does not repeat vertices.
Cycle	A path that starts and ends at the same vertex.
Complete	Every vertex is connected to every other vertex.
Connected	Every vertex is reachable from every other vertex.
Bipartite	Vertices are separable into two sets such that no two vertices from the same set are connected.
Tree	A connected graph with no cycles.
Eulerian trail	A trail where every edge is used exactly once.
Hamiltonian path	A path where every vertex is used exactly once.

©2025 Jedediyah Williams
This work is licensed under the Creative Commons
Attribution-NonCommercial-ShareAlike 4.0 International License.

To view a copy of this license, visit https://creativecommons.org/licenses/by-nc-sa/4.0/.