Computing and Data Science

Regression

These exercises are intended to be done in a spreadsheet and Desmos, without automated regression tools.
  1. For the following data:
    \(x\) 3.0 5.0 6.0 8.0 9.0
    \(y\) 5.0 5.8 5.5 6.0 7.6
    we are using the model: \[ \hat{y} = 3 + \frac{x}{2} \]
    1. What does the model predict for \(x=7\)?
    2. For each input \(x_i\), calculate the prediction \(\hat{y}_{i}\).
    3. For each prediction \(\hat{y}_{i}\), calculate the residual error \(e_i = y_i - \hat{y}_i\).
    4. Calculate the sum of squared errors.
    5. Calculate the mean squared error.
    6. Find the parameters of a linear model \[\hat{y} = \hat{\beta}_{0} + \hat{\beta}_{1}x\] that fits the data with a smaller MSE than the model above.
    7. Redo steps a through e using a spreadsheet with formulas. Parameters \(\hat{\beta}_0\) and \(\hat{\beta}_1\) should be in cells that are referenced in the formulas so that you can change those values and see the effects propogate through every calculation.
  2. Given:

    \(x\) 4 5 6
    \(y\) \(y_1\) \(y_2\) \(y_3\)

    1. Find values of \(y\) to complete the data set such that the model \(\hat{y} = 10 + \frac{x}{2} \) has \(SSE=2\).
    2. Find the \(MSE\) using your data points.
  3. Here is a a dataset of water depths: Depths
    1. Copy and paste the data into Desmos to create a scatter plot. This should create a table.
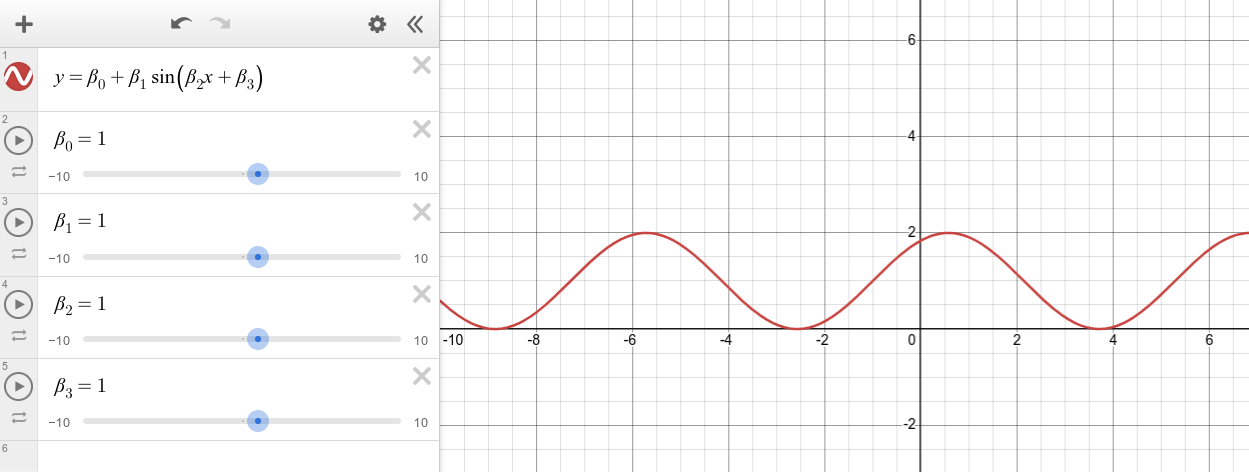
    2. We are going to adjust, by hand, the parameters of a sinusoidal model (do not do an automated regression): \[ \hat{y} = \hat{\beta}_0 + \hat{\beta}_1 \sin( \hat{\beta}_2 t + \hat{\beta}_3 ) \] Add this model to Desmos as shown (you can type "beta" to create a \(\beta\)).
    3. Add the sliders and adjust them until your model appears to fit the data. Record your best hand-fit parameter values.
    4. Interpret each of the parameters in the context of the model. For example, \(\hat{\beta}_{0}\) represents a particular property of the tide which you can describe.
    5. Our model has four parameters. Could you still model the tide well enough with only three?
  4. Consider a pendulum with mass, length, and initial angle.
    1. Create an experiment to collect data on how each of these three features affects the period of a pendulum.
    2. Plot the period as a function of each feature. For each plot, choose an appropriate model and fit that model to your data.
    3. Decide which feature(s) to combine into a single model, and validate your model by making predictions for unknown values and testing your predictions.
  5. How high does a bouncy ball bounce? You may work in groups of 2 or 3. Your report should *at least* include:
    1. A brief but informative description of your experiment
    2. Your data
    3. Details of your model
    4. Details about how you determined your model coefficient(s) with a regression
    5. Use data splitting as a technique for validating your model
    The purpose of this lab is to experience the most fundamental aspects of regression, so do as much of your modeling as you can by hand. For example, if you use a spreadsheet then try to avoid built-in functions. Don't do your regression with software unless you have to. Try to be as clear as you can about the steps you took with data splitting so that I can give you feedback.